[문제]
https://www.acmicpc.net/problem/2609
2609번: 최대공약수와 최소공배수
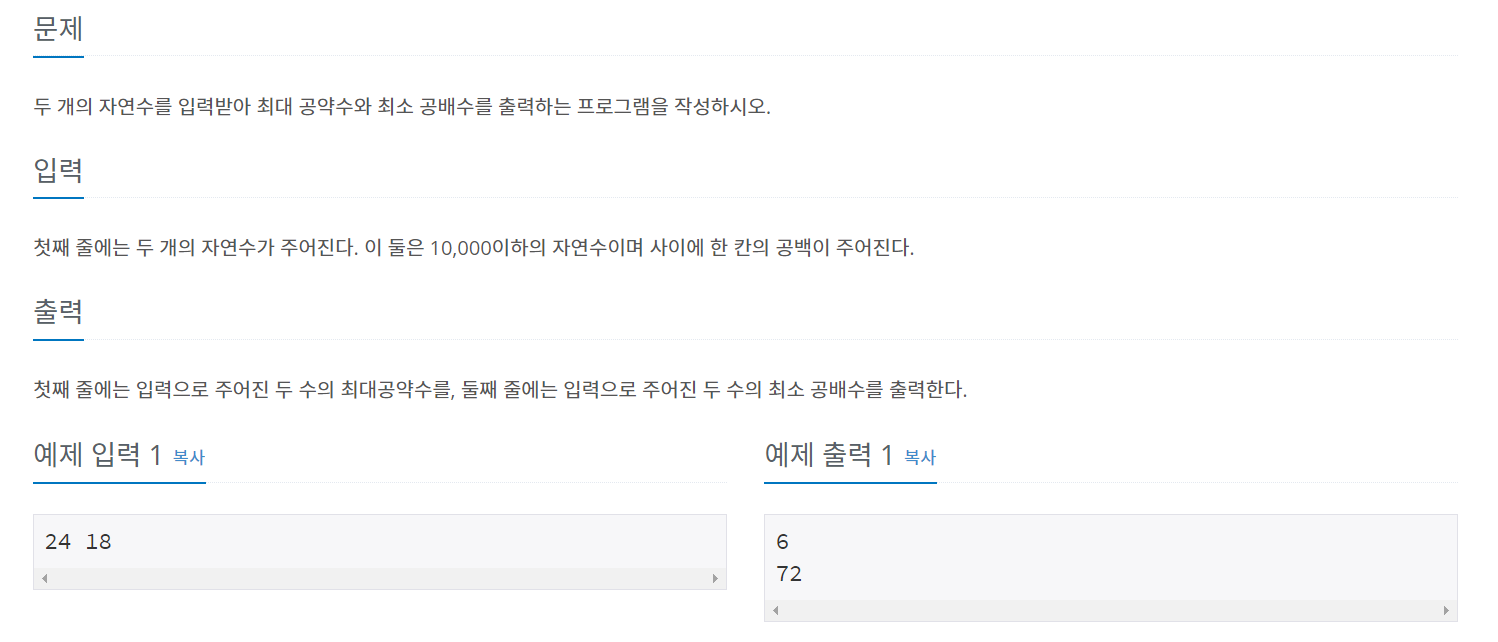
첫째 줄에는 입력으로 주어진 두 수의 최대공약수를, 둘째 줄에는 입력으로 주어진 두 수의 최소 공배수를 출력한다.
www.acmicpc.net
[풀이]
1. 최대공약수 (GCD: Greates Common Divisor)
최대공약수를 구할 때 반복문을 사용해 알고리즘을 짰었는데 언뜻 봐도 시간복잡도가 O(n)이나 된다..
시간복잡도를 줄일 다른 알고리즘을 찾아보니 유클리드 호제법(Euclidean algorithm)이 있었다!!
유클리드 호제법(Euclidean algorithm)
원리 : a, b의 최대공약수 == b와 a%b의 최대공약수
-> GCD(a, b) = GCD(b, a%b)
a%b가 0이 될 경우 해당 b가 최대공약수이다.
ex) GCD(24, 18) = GCD(18, 6) = GCD(6, 0)
마지막에 a%b가 0이 되었기 때문에 24와 18의 GCD는 6이다.
2. 최소공배수 (LCM: Least Common Multiple)
최소공배수는 유클리드 호제법을 이용해 구한 최대공약수를 이용해 쉽게 구할 수 있다.
a = x * GCD(a, b) 이고 b = y * GCD(a, b) 이기 때문에 최소공배수는 a*b / GCD(a, b) 이다.
해당 수는 a, b 중 어느 수로 나눠도 나누어 떨어지고, 나누어 떨어지는 숫자 중 가장 작은 수이기 때문이다.
-> LCM(a, b) = GCD * (a/GCD) * (b/GCD)
[코드]
def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
def lcm(a, b):
g = gcd(a, b)
return int(g * (a/g) * (b/g))
if __name__ == '__main__':
a, b = map(int, input().split())
print(gcd(a, b))
print(lcm(a, b))'문제풀이 > BOJ' 카테고리의 다른 글
| [Python] BOJ/백준 1009번 분산처리 (0) | 2021.06.09 |
|---|---|
| [Python] BOJ/백준 1267번 핸드폰 요금 (0) | 2021.06.08 |
| [Python] BOJ/백준 11653번 소인수분해 (0) | 2021.06.04 |
| [Python] BOJ/백준 7568번 덩치 (0) | 2021.06.04 |
| [Python] BOJ/백준 17496번 스타후르츠 (0) | 2021.06.02 |
